يكي از مشكلات مهم جامعه نجوم آماتوري ايران، نوابيغ نجومي هستند. مقاله زير خيلي برام جالب بود، البته تايپش كلي مصيبت داشت برام. منبع مقاله خبرنامه انجمن رياضي ايران، شماره 103، بهار 1384.
نوابيغ
عفّت چهره گشا و سيّد عباداله محموديان
چكيده
احتمالاً تا به حال شنيده ايد كه حدس معروف گلدباخ هنوز اثبات نشده است. پس رياضي دان ها چه مي كنند؟ آيا كسي را مي شناسيد كه به فكر اثبات آن باشد؟ تابعي سراغ داريد كه به كمك آن بتوان اعداد اوّل را تشخيص داد؟ اگر كسي ادّعا كند كه مي تواند هر زاويه دلخواه را تنها با كمك خط كش و پرگار به سه قسمت مساوي تقسيم كند در مورد او چه فكر مي كنيد؟ آيا او يك نابغه است؟
مقدّمه
مي خواهيم در مورد نوابيغ صحبت كنيم. نه اشتباه نكنيد نوابيغ جمع نابغه نيست. در واقع نوابيغ افرادي هستند كه ادّعاي نبوغ دارند و معمولاً يك جايي يك مسأله با جايزه 1 ميليون دلاري ديده اند يا در دبيرستان از دبير رياضي خود شنيده اند كه فلان مسأله قرن ها حل نشده باقي مانده است. بعد سعي مي كنند آن را حل كنندو حتّي ممكن است سال هاي سال عمر عزيزشان را بر سر اين كار تلف كنند. اين اشخاص در تمام كشورها يافت مي شوند. در كشور ما نيز نوابيغ پيدا مي شوند. تجربه چند سال اخير، ما را بر آن داشت كه به دلايلي كه توضيح خواهيم داد اين مقاله را بنويسيم. در اين مقاله حروف لاتين را براي ارجاع به بعضي از اين اشخاص به كار برده ايم و به دلايلي كه در متن مقاله روشن خواهد شد از آوردن مشخصات آنان خودداري كرده ايم.
1. دسته بندي نوابيغ
ما نوابيغ را به سه دسته تقسيم مي كنيم :
* كساني كه سعي مي كنند ناممكن ها را ممكن سازند!
اين دسته به تثليث گرها يا Trisectne معروفند. تثليت گر يعني كسي كه سعي مي كند فقط با كمك خط كش و پرگار زاويه را به سه قسمت مساوي تقسيم كند. امّا غير از اين ها افراد ديگري هم جزء اين دسته هستند. مثلاً كساني كه سعي مي كنند فرمول محيط بيضي را كشف كنند يا بر روي روش تربيع دايره و تضعيف مكعب و ... كار كنند. براي اطّلاع از ناممكن بودن اين ها به كتاب مرجع مراجعه شود. يا حتّي هستند كساني كه سعي مي كنند فقط با دو رنگ هر نقشه اي را رنگ كنند!
* مدّعيان حل مسأله هاي حل نشده معروف
اين دسته نسبت به دسته اوّل كمي معقول ترند. ايشان آدم هايي هستند كه سعي مي كنند مسأله هاي بزرگ حل نشده را كه به پيش زمينه هاي رياضي قوي نياز دارند، بدون داشتن آن پيش زمينه ها حل كنند. مثلاً فرضيه كلدباخ، فرمول توليد اعداد اول و ....
* بنيان گذاران نظريه هاي بي اساس
اين افراد مدّعي بنيان گذاري نشريه هاي بي پايه ولي از نظر خودشان بسيار مهم هستند، كه حتّي مي تواند رياضي را متحوّل كند. در بين اين دسته كساني هستند كه با شنيدن ادّعايشان عصبي مي شويد. شايد هم كلّي بخنديد. مثل كسي كه ادّعا مي كند :
«پايان امسال مي توانم نظريه نامرئي كردن فيزيكي اشياء را كامل كنم.» (X) و يا «شايد برايتان باور نكردني باشد كه اين كتاب و اين تحقيقات را يك جوان بيست ساله انجام داده باشد كه حتّي اثبات رياضي وجود وجدانيّت خداوند كه بزرگترين آرزوي يكتا پرستان جهان اسلام است را از طريق اين نظريه كشف نموده باشد. (Y)
يكي از كارمندان دبيرخانه انجمن رياضي ايران نقل مي كند : چندي پيش شخصي متولد 1291 (با حدود 91 سال سن) باتّفاق دخترش به انجمن رياضي ايران مراجعه كردند كه مدعي بودند :
«براي هر عدد، عددي يافته است كه حاصل جمع آن با عدد داده شده و حاصل ضرب آن با همان عدد، يكسان است متشابهاً، حاصل تفريق و حاصل تقسيم.»
او مدّعي بود كه اين آموزش رياضي را متحوّل مي كند و جوان ها را از آلودگي نجات مي دهد. (مي گفت: با اين روش آموزش، جوان ها تا قبل از 18 سالگي دكتراي خود را مي گيرند و ديگر آلوده نمي شوند!). هم چنين همين شخص جداولي با اعداد چندين رقمي عجيب (جداول مربعي) رسم كرده بود كه به اين اعداد نام «نيرو» داده بود و مي گفت اين نيروها از تمام جهات با هم برابرند. ايشان مايل بودند كه اين اكتشافات به نام خودشان ثبت شود و دنبال راهي بودند كه از اين مطالب شخص ديگري به نام خود سوء استفاده نكند. (اين نكته در اغلب اين افراد مشابه است.)
2. كالبد شكافي نوابيغ
البته نوابيغ در رشته هاي ديگر نيز وجود دارند. همكاري تعريف مي كرد كه يك نفر در مراجعه حضوري به شوراي شهر تقاضا كرد كه از طرح پژوهشي ايشان حمايت شود. اين طرح روش آموزش صحبت كردن به بلبل ها بود! ايشان بلبلي را هم همراه برده بود و ادّعا مي كرد كه حرف مي زند ولي به خاطر ترس از جمعيّت از نطق كردن وامانده است.
مقاله هايي وجود دارند كه در آن ها رفتار نوابيغ مورد بررسي قرار گرفته اند. مثل مقاله ]يك[ كه در آن چنين آمده است : «يكي از مشخصه هاي نوابيغ رياضي، مانند ساير انواع نوابيغ، اين است كه به موفّقيت هاي كوچك قانع نيستند. حل مسائل معمولي آن ها را راضي نمي كند چرا كه دون شأن آن هاست. مي خواهند حرف مهم بزنند يا پنبه حرف هاي مهم را بزنند. بيشتر دوست دارند مسائلي را حل كنند كه ديگران ثابت كرده اند نمي توان آن ها را حل كرد ... خلاصه مي خواهند كاري بكنند كارستان. و از حيث شجاعت و بلند پروازي دست كمي از دانشمندان درست و حسابي ندارند. ولي متأسفانه شباهتشان با نوابغ واقعي، در همين يك صفت خلاصه مي شود.» براي علاقه مندان، مطالعه اين مقاله را پيشنهاد مي كنيم. نويسنده آن Underwood Dudley همان نويسنده كتاب هاي ]1[ و ]2[ است. ايشان بيش از ربع قرن است كه مشغول مطالعه رفتار و كردار نوابيغ رياضي هستند.
3. نوابيغ و پخش نظراتشان
* مراجعه به هر جا و هر كس
اغلب نوابيغ چيز زيادي از رياضي نمي دانند ولي علاقه مندند در اين زمينه كار كنند. شايد بپرسيد اصلاً چرا رفتيم سراغ اين آدم ها؟ جواب را بايد مراجعه بيش از حدّ اين افراد به انجمن رياضي و نشريات وابسته به آن و مديران گروه هاي رياضي دانست. مثلاً به عنوان رئيس انجمن رياضي لااقل از دفتر پنج مقام مختلف مملكتي براي بررسي ادّعاي فقط يكي از ايشان نامه هائي همراه با ضمايم فراوان رسيده است (به پيوست 3 مراجعه شود). راستش اين افراد خيلي تنها هستند. يكي از آنها (X) نوشته بود : «از اين كه با شما بزرگوار در ارتباط هستم از ته دل خوشحالم و اميدوارم اين ارتباط هم چنان پايدار باشد و از اين حالت يك طرفه شدن خارج شده و .... رياضيدان هاي بزرگ به حق نمي توانند وقت كافي براي رسيدگي به اين موضوعات بگذارند. دانشجويان رياضي نيز اغلب نمي دانند كه چنين افرادي هم وجود دارند. البته مشكل به اين جا ختم نمي شود. بين نوابيغ بعضاً كساني يافت مي شوند كه مستعد ايجاد مشكلات بسيار بزرگي براي رياضيدانان و بقيّه آدم ها هستند و اگر در برخورد با اين افراد دقّت لازم را به عمل نياورند بايد منتظر يك دردسر خيلي بزرگ باشيد كه در ادامه مقاله بيشتر متوجّه اهميّت موضوع خواهيم شد.
همان طور كه قبلاً اشاره شد يك گروه عمده از نوابيغ، تثليت گرها هستند كه اغلب آنها در دوران دبيرستان با مسأله تثليث مواجه مي شوند. مي دانيم كه ثابت شده است تيليث زاويه تنها با خط كش و پرگار امكان پذير نيست. مثلاً به كتاب «رياضيات چيست» (دو) فصل سوّم صفحات 147 و 148 رجوع كنيد. ولي اين افراد يا نمي دانند كه چنين اثباتي وجود دارد و يا نمي توانند معناي «امكان پذير بودن» در رياضيات را درك كنند. آيا تا به حال با كسي مواجه شده ايد كه متوجّه نشود فقط با يك شمع و يا با يك چراغ موشي نمي توان يك تيرآهن را گداخت؟!
در برخورد با يك تثليت گر، خواندن روش تثليت وي عملاً كار بيهوده اي است. علاوه بر اين، اين افراد معمولاً نمودارهاي پيچيده اي رسم مي كنند كه سر درآوردن از آن ها كار سختي است. جالب اينجاست كه حتّي وقتي اثبات امكان ناپذير بودن تثليت را برايشان بفرستيد باز هم اصرار دارند كه روش آن ها مورد مطالعه قرار بگيرد! نمونه اي از اين افراد خانم Z (دبير رياضي) بود كه پس از ارائه برهان توسّط يكي از نويسندگان (پيوست 2) باز هم اصرار بر خواندن مقاله اش داشت. ايشان حتّي تهديد كرد كه اگر مقاله اش را نخوانيم ما را به صاحب شب قدر مي سپارد.
* مراجعه به مقامات
يكي ديگر از ويژگي هاي نوابيغ اين است كه براي ثبت تئوري خود سراغ مقامات و مسئولين رده بالاي كشوري مي روند و حتّي ممكن است به بالاترين مقام كشور نيز رجوع كنند. يك نمونه از اين افراد آقاي U است كه ادّعا مي كند فرضيه گلدباخ را ثابت كرده است. ايشان براي اثبات ادّعاي خود حتّي به رهبر و رئيس جمهور و رئيس قوّه قضائيه نيز نامه نوشته اند. گوشه هايي از نامه پرسوز و گداز اين سودازده رياضي را برايتان مي آوريم :
« ... كار جديدم اثبات فرضيه تاريخي گلدباخ است. اين فرضيه به مدّت 261 سال لاينحل باقي مانده بود و دانشمندان نامداري چون اولر، گاوس، ويتوگرادف و هزاران رياضي دان ديگر در طول اين 5/2 قرن براي حل آن كوشيدند ولي ناكام ماندند .... بنده پس از دوازده سال تلاش در سال 1380 (سال مولي علي (ع)) موفق به اثبات قطعي آن گرديدم. اثبات بنده در 286 مركز علمي و دانشگاهي جهان بررسي و كوچكترين ايرادي بر آن وارد نگرديد. البتّه آمريكا پرداخت جايزه 1 ميليون دلاري بنده را مشروط به پذيرش تبعيت آمريكا نمود ....»
نوابيغ ممكن است هر كدام به تنهائي به مراجع زيادي رجوع كنند كه با اين عمل با توجّه به نامهه اي مختلف موجب اتلاف وقت بزرگي مي شوند. مثلاً موردي به نام آقاي X مقاله خود را به 100 مرجع مختلف فرستاده بود كه به قول خود چون از نوشتن همه آن ها عاجز بود به ناچار به دستگاه كپي متوسّل شده بود! اين آدم ها از رجوع به مقامات و مسئولين خسته نمي شوند و اگر در برخورد با اين آدم ها دقّت نكنيم ممكن است دچار يك دردسر اساسي شويم. مثلاً يكي از اساتيد دانشگاه در جواب يكي از همين نوابيغ مقاله اي را برايش فرستاده بود كه به خاطر اين كار آن شخص ايشان را به دادگاه كشاند.
* انتشار جزوات و كتاب ها
در برخي موارد نوابيغ براي عرضه نظريه هاي به قول خود «شگفت انگيزشان» دست به نشر كتاب در تيتراژ چند هزار جلدي مي زنند. حداقل دو مورد آن را اخيراً در كشورشاهد هستيم. يكي از اين دو نفري كه كتاب منتشر كرده است يك دانش آموز مقطع پيش دانشگاهي به نام Y است كه ادّعا مي كند :
«جلد اوّل اين كتاب علاوه بر بعد رياضياتش، بعد ديگري نيز دارد كه استفاده از آن در بحث هاي فلسفي و عرفاني از جمله اثبات روح، برزخ و حقيقت زنده شدن مردگان مي توان نام برد و ....»
و ديگري نيز كه كتاب خود را در دوران دبيرستان نوشته است، ادّعا مي كند كه :
«... در خلال اين تحقيقات موّفق به كشف رياضي اثبات وجود وحدانيّت خداوند متعال نيز شدم كه اميدوارم جوّ به خواب رفته علمي كشور را بيدار نمايد و ....» (X).
حتماً تا به حال خبر كشفيّات جديد در علم را از رسانه هاي گروهي از جمله اخبار سراسري شنيده ايد. ما مواردي را سراغ داريم كه اين افراد از طريق همين رسانه ها كه مردم، بسياري به بخش خبرهاي علمي آنها اعتماد دارند، خبر به اصطلاح كشفيات خود را به اطلاع عموم مي رسانند. مثل خبر حل فرضيه گلدباخ توسط آقاي X كه حداقل از يكي از شبكه هاي تلويزيوني پخش شده است. هم چنين ايشان چندين مصاحبه مطبوعاتي چاپ شده در روزنامه هاي كثيرالانتشار را در پرونده خود دارد.
خلاصه اين كه اگر پاي درددل بعضي از آن ها بنشينيد، ممكن است يك نطق مفصّل در مورد فرار مغزها به خاطر عدم حمايت از نابغه هائي مثل ايشان بكنند. اخيراً اغلب آن ها اين ادّعا را نيز بر ادّعاهاي فبلي خود اضافه كرده اند. مثل آقاي U كه حتّي ادّعا مي كرد از كشور آمريكا و انگلستان دعوتنامه براي ايشان و خانواده شان فرستاده شده و به ايشان ويزاي آمريكا همراه با چهار بليط مجّاني هواپيما پيشنهاد كرده اند. وي يك ديسكت حاوي اين ادّعا را به همه جا فرستاده بود كه ما با ديدن يك ديسكت متوجّه شديم موضوع چيزي نيست به جز چند پيام تبليغاتي كه براي شركت در قرعه كشي براي اخذ ويزا و يا مسافرت تفريحي معمولاً به تمامي كاربران Yahoo فرستاده مي شود!
راه هاي پيشنهادي براي مواجهه با نوابيغ
با توضيحاتي كه مطرح شد، حدس مي زنيم همه شما خوانندگان مثل ما معتقديد بهتر است فكري به حال اين افراد بكنيم تا هم بسياري را از درگير شدن با آن ها نجات دهيم و هم خود اين افراد دست از «آب در هاون كوبيدن» بردارند. مثلاً يكي از ايشان كه دبير رياضي هم است، ابراز مي دارد :
«اكنون بنده نه تنها از سال ها زحمت و تحقيقات ام خوشحال نيستم بلكه به شدّت غمگينم و فكر مي كنم راه اشتباهي رفته ام كه جذب علم و دانش و افتخار آفريني براي كشورم شده ام. چون از اوّلين روز اتمام اثبات و اعلام آن به دانشگاه ها تمام اضافه كاري ها و كمك درآمدها و كلاس هاي اضافه ام را تعطيل كرده و علاوه بر آن مخارج بسياري نيز در اين راه هزينه نمودم. البتّه هراسي نداشتم چون علاوه بر افتخار كشورم، يك ميليون دلار جايزه را نيز در دستم مي ديدم. لذا از قرض كردن نيز هراسي نكردم. امّا اكنون خوار و خفيف شده ام. هر روز از صاحب خانه فرار مي كنم كه اجازه چند ماه را نپرداخته ام. به اكثر آشنايان بدهكارم و شايد چند روز ديگر جهت بدهي به زندان هم بروم ... به زندان بروم يا به آمريكا بروم و تبعه آنجا شوم (البته بليط هواپيما و كارت اعتباري نيز برايم فرستاده اند كه در ديسك همراه نامه موجود است) يا در كشورم بمانم و اثبات قطعي فرضيه گلدباخ را با خودم به آن دنيا ببرم ....» (U).
ما مخاطبين اين افراد را به چهار دسته تقسيم مي كنيم :
* دسته اوّل، كساني كه وقت كافي براي پاسخ گويي به اين افراد را ندارند. به ايشان توصيه مي كنيم همين مقاله را در پاسخ آن ها ارسال كنند. چه بسا با مطالعه اين مقاله بسياري از مدّعيان پي به اشتباه خود برده و كار خاتمه يابد.
* دسته دوّم، بعضي از رسانه ها هستند كه با پخش خبرهاي غلط يا چاپ كتاب هاي خالي از هر گونه بار علمي موجب گمراهي اذهان عمومي مي شوند. با توجّه به رسالت مهم رسانه ها در اطلاع رساني چاپ اين گونه خبرها از طرف برخي از اين رسانه ها بسيار تأسف برانگيز است. رسانه ها قبل از نشر هر گونه خبر علمي بايد آن را توسط يك كارشناس مورد بررسي قرار دهند و در صورت اطمينان از صحّت، اقدام به پخش آن نمايند.
* دسته سوّم، دفاتر مقامات و مسئولين مملكتي است كه تصوّر مي كنيم در موارد بسياري تشخيص اين عدّه از نوابيغ برايشان كاري دشوار است. مثلاً يكي از مسئولان با ارسال ادّعاي آقاي X كه قبلاً ديديم ادّعاي «نامرئي كردن فيزيكي اشيا را» داشت به وزير علوم، تحقيقات و فن آوري، نوشته بودند «به پيوست تصويرنامه آقاي X از محققين، نظريه پردازان و طراحان رياضي كشور تقديم مي گردد. نامبرده از نوجواني تا كنون موفّق به كشفيات و ارائه طرح هايي در زمينه علوم رياضي گرديده اند ليكن براي ادامه فعّاليت هاي خود نيازمند مساعدت و حمايت مي باشند. نامه پيوست و ضميمه آن خود گوياي تمام توانايي ها و نبوغ نامبرده است. انتظار دارم درخواست ايشان مورد نظر قرار بگيرد كه قطعاً در پيشبرد اهداف علمي ايشان در نگاهي وسيع تر، كشور ايران بسيار سودبخش خواهد بود.»
هم چنين از طرف دفتر يكي از مقامات بلندپايه كشور پي نوشتي درباره ادّعاي آقاي X به انجمن رياضي ايران نوشته اند : «از ارسال كتاب تأليفي آقاي X محقق جوان و عزيزمان تشكر و قدرداني مي شود. براي ايشان از خداوند بزرگ آرزوي توفيق بيشتر را دارم.» لذا به دفتر مقامات پيشنهاد مي كنيم اگر بررسي اين ادعاها برايشان مهم است، از تعدادي از كارشناسان دعوت كنند كه به رسيدگي آن ها بپردازند. انجمن هاي علمي مي توانند معرّف اين كارشناس ها باشند.
* دسته چهارم، كساني كه علاقه مند به اين مسائل هستند و وقت كافي براي رسيدگي به آن ها را دارند. اگر شما هم جزء اين گروه هستيد، پيشنهاد مي كنيم مقاله (يك) را مطالعه كنيد. همان طور كه گفتيم نويسنده مقاله فوق حدود 25 سال در اين زمينه كار كرده و راه هاي مختلفي را در برخورد با اين افراد امتحان كرده است. ايشان نتيجه تجربيّات خود را در اين مقاله چنين بيان مي كند :
«سرانجام وقت آن رسيده كه بگويم با تثليت گرها چگونه بايد برخورد كرد. امّا بگذاريد اوّل بگوييم چگونه نبايد برخورد كرد. يك راه خلاصي موقّت از چنگ تثليت گرها آن است كه بگوييد : خوب تا اينجايش قبول، امّا مي دانيد كه بايد براي درست بودنش برهان داشته باشيد. يعني يك سري حكم ها و استدلال هايي نظير آنچه در كتاب هندسه قديميتان داشتيد. تثليث گر از نزدتان مي رود ولي به همراه برهان برمي گردد. در اين مرحله ممكن است بگوييد : خوب، حالا نگاهي به آن بياندازيم، اشتباه آن را بيابيد و به تثليت گر گوشزد كنيد.
تثليث گر اين بار هم مي رود ولي باز همراه با برهان تجديدنظر شده اي برمي گردد كه طولاني تر، پچيده تر و يافتن اشتباهش دشوارتر است. تجديدنظرهاي پياپي در برهان، كار را به جايي مي كشاند كه ديگر نتوانيد يا نخواهيد اشتباه آن را پيدا كنيد. قدم بعدي كه آن نيز خطاست، اين است كه بگوييد :
راستش من وقت بررسي اين برهان را ندارم ولي مي دانيد كه شخصي به نام وانيتيسل در سال 1837 ثابت كرده كه زاويه را نمي توان با خط كش و پرگار تثليث كرد. برهان او موجود است، اين هم برهان شما؛ هر دوي اين ها نمي توانند درست باشند؛ پس چاره اي نيست جز اين كه شما در برهان وانيتيسل اشتباهي پيدا كنيد. اين كار هم تثليثت گر را از سرتان باز مي كند. ولي او دير يا زود بر مي گردد با رديه اي بر برهان وانتسل در قالب چنان عباراتي كه درك معني شان ناممكن است. هيچ چيز نمي تواند راه را بر تثليث گر از خود گذشته ببندد.
پس در برخورد با تثليث گر چه بايد كرد؟ به اوّلين نامه تثليث گر، اگر مطمئن شديد كه خوبي تقريب يا سادگي روش يا هوشمندي او در يافتن تقريبي جديد قابل توجه است، مودّبانه جواب بدهيد. به همراه نامه، برايش فهرستي كامپيوتري از اشتباهات موجود در ترسيم براي زاويه هاي مختلف بفرستيد. من معمولاً فهرست را براي 0 تا 180 درجه، با فواصل 3 درجه اي تهيّه مي كنيم. اين كار مهم است زيرا هنوز كامپيوتر قدرت آن را دارد كه احساس احترام و ابهتي در افراد ايجاد كند. همچنين با آن نامه چند تثليث تقريبي ديگر را بفرستيد با تذكّري از اين قبيل كه فكر كردم شايد علاقه مند باشيد ديگران چه تثليث هاي تقريبي به دست آورده اند. در سال هاي اخير با استفاده از اين روش ميزان موفّقيتم بالا رفته است. يادم هست كه اوّلين موفّقيّت تا چه حد مايه رضايت خاطرم شد. مهندسي در شهر نيوجرسي كتاب بزرگي با جلد مقوّايي در حجم بيش از 250 صفحه تهيّه كرده بود كه عنوان ماجراهاي هندسه روي جلد آن با حروف زركوب نقش بسته بود. به نظرم رسيد كسي كه اين همه براي تثليث مايه گذاشته باشد، راه نجاتي ندارد. ولي او ضمن پاسخ نامه ام نوشت : همين قدر كه توانسته ام به تقريبي برسم راضي هستم و ديگر آن را كنار مي گذارم. اين بار روحم از نفرين به دور ماند! اخيراً چند موفّقيّت ديگر هم داشته ام و شايد برخي از اين تثليت گرهاي لب فرو بسته، متقاعد هم شده باشند، اگر با اين روش كاري از پيش نرفت، آن وقت بي رحم باشيد. نامه و برخورنده اي بنويسيد، به اين قصد كه طرف از شما بدش بيايد. ديگر به هيچ قيمتي مزاحم شما نخواهد شد و شايد بخشي از نفرتش منجر به بي علاقگي نسبت به رياضيدانان و بي ميلي به ادامه كار تثليث شود، زيرا معمولاً انسان اگر بتواند، از كاري كه مايه آزارش شود خودداري مي كند. اگر همه همين روش را در پيش مي گرفتند نسل تثليث گرها تحليل مي رفت و منقرض مي شد. در آن صورت كساني كه سودازدگي جزء سرشتشان است مزاحم اقتصاد دان ها، فيزيك دان ها يا علماي الهيّات مي شدند و ما مي توانستيم در آرامش و امنيّت زندگي كنيم و مطمئن باشيم كه از اين پس هيچ سودازده اي به سراغمان نخواهد آمد. در اين جا به طور خاص در مورد تثليث گرها صحبت شده است، امّا حتماً شما آنقدر وارد هستيد كه با استفاده از آن، روش برخورد با ساير نوابيغ را نيز بيابيد.»
موخره، از خوانندگان محترم تقاضا مي شود اگر خاطره اي از نوابيغ دارند حدود يك يا دو صفحه به اينجانبان ارسال دارند تا در ضميمه اين مقاله بيايد. به پيوست نمونه اي از نامه هاي ارسال شده در رابطه با نوابيغ ضميمه شده است.
پيوست : چند نمونه از نامه هاي ارسالي درباره مدّعيان
* پيوست 1 : آقاي ... مقاله شما را در ادعاي كشف فرمول محاسبه محيط بيضي مشاهده كردم. به اطلاع مي رساند كه انجمن رياضي ايران بر اساس تجربه هاي قبلي به اين گونه مدعيان پيشنهاد مي كند كه با اساتيد دانشگاه ها مستقيماً مكاتبه نمايند. اما اين جانب خود به عنوان يك عضو هيأت علمي دانشگاه، نظرم را ذيلاً مكتوب مي نمايم.
لازمه محاسبه فرمول دقيق محيط بيضي محاسبه انتگرال هايي مانند انتگرال زير است كه ثابت شده است محاسبه آن بر حسب توابع معمولي امكان پذير نيست.
نوابيغ
عفّت چهره گشا و سيّد عباداله محموديان
چكيده
احتمالاً تا به حال شنيده ايد كه حدس معروف گلدباخ هنوز اثبات نشده است. پس رياضي دان ها چه مي كنند؟ آيا كسي را مي شناسيد كه به فكر اثبات آن باشد؟ تابعي سراغ داريد كه به كمك آن بتوان اعداد اوّل را تشخيص داد؟ اگر كسي ادّعا كند كه مي تواند هر زاويه دلخواه را تنها با كمك خط كش و پرگار به سه قسمت مساوي تقسيم كند در مورد او چه فكر مي كنيد؟ آيا او يك نابغه است؟
مقدّمه
مي خواهيم در مورد نوابيغ صحبت كنيم. نه اشتباه نكنيد نوابيغ جمع نابغه نيست. در واقع نوابيغ افرادي هستند كه ادّعاي نبوغ دارند و معمولاً يك جايي يك مسأله با جايزه 1 ميليون دلاري ديده اند يا در دبيرستان از دبير رياضي خود شنيده اند كه فلان مسأله قرن ها حل نشده باقي مانده است. بعد سعي مي كنند آن را حل كنندو حتّي ممكن است سال هاي سال عمر عزيزشان را بر سر اين كار تلف كنند. اين اشخاص در تمام كشورها يافت مي شوند. در كشور ما نيز نوابيغ پيدا مي شوند. تجربه چند سال اخير، ما را بر آن داشت كه به دلايلي كه توضيح خواهيم داد اين مقاله را بنويسيم. در اين مقاله حروف لاتين را براي ارجاع به بعضي از اين اشخاص به كار برده ايم و به دلايلي كه در متن مقاله روشن خواهد شد از آوردن مشخصات آنان خودداري كرده ايم.
1. دسته بندي نوابيغ
ما نوابيغ را به سه دسته تقسيم مي كنيم :
* كساني كه سعي مي كنند ناممكن ها را ممكن سازند!
اين دسته به تثليث گرها يا Trisectne معروفند. تثليت گر يعني كسي كه سعي مي كند فقط با كمك خط كش و پرگار زاويه را به سه قسمت مساوي تقسيم كند. امّا غير از اين ها افراد ديگري هم جزء اين دسته هستند. مثلاً كساني كه سعي مي كنند فرمول محيط بيضي را كشف كنند يا بر روي روش تربيع دايره و تضعيف مكعب و ... كار كنند. براي اطّلاع از ناممكن بودن اين ها به كتاب مرجع مراجعه شود. يا حتّي هستند كساني كه سعي مي كنند فقط با دو رنگ هر نقشه اي را رنگ كنند!
* مدّعيان حل مسأله هاي حل نشده معروف
اين دسته نسبت به دسته اوّل كمي معقول ترند. ايشان آدم هايي هستند كه سعي مي كنند مسأله هاي بزرگ حل نشده را كه به پيش زمينه هاي رياضي قوي نياز دارند، بدون داشتن آن پيش زمينه ها حل كنند. مثلاً فرضيه كلدباخ، فرمول توليد اعداد اول و ....
* بنيان گذاران نظريه هاي بي اساس
اين افراد مدّعي بنيان گذاري نشريه هاي بي پايه ولي از نظر خودشان بسيار مهم هستند، كه حتّي مي تواند رياضي را متحوّل كند. در بين اين دسته كساني هستند كه با شنيدن ادّعايشان عصبي مي شويد. شايد هم كلّي بخنديد. مثل كسي كه ادّعا مي كند :
«پايان امسال مي توانم نظريه نامرئي كردن فيزيكي اشياء را كامل كنم.» (X) و يا «شايد برايتان باور نكردني باشد كه اين كتاب و اين تحقيقات را يك جوان بيست ساله انجام داده باشد كه حتّي اثبات رياضي وجود وجدانيّت خداوند كه بزرگترين آرزوي يكتا پرستان جهان اسلام است را از طريق اين نظريه كشف نموده باشد. (Y)
يكي از كارمندان دبيرخانه انجمن رياضي ايران نقل مي كند : چندي پيش شخصي متولد 1291 (با حدود 91 سال سن) باتّفاق دخترش به انجمن رياضي ايران مراجعه كردند كه مدعي بودند :
«براي هر عدد، عددي يافته است كه حاصل جمع آن با عدد داده شده و حاصل ضرب آن با همان عدد، يكسان است متشابهاً، حاصل تفريق و حاصل تقسيم.»
او مدّعي بود كه اين آموزش رياضي را متحوّل مي كند و جوان ها را از آلودگي نجات مي دهد. (مي گفت: با اين روش آموزش، جوان ها تا قبل از 18 سالگي دكتراي خود را مي گيرند و ديگر آلوده نمي شوند!). هم چنين همين شخص جداولي با اعداد چندين رقمي عجيب (جداول مربعي) رسم كرده بود كه به اين اعداد نام «نيرو» داده بود و مي گفت اين نيروها از تمام جهات با هم برابرند. ايشان مايل بودند كه اين اكتشافات به نام خودشان ثبت شود و دنبال راهي بودند كه از اين مطالب شخص ديگري به نام خود سوء استفاده نكند. (اين نكته در اغلب اين افراد مشابه است.)
2. كالبد شكافي نوابيغ
البته نوابيغ در رشته هاي ديگر نيز وجود دارند. همكاري تعريف مي كرد كه يك نفر در مراجعه حضوري به شوراي شهر تقاضا كرد كه از طرح پژوهشي ايشان حمايت شود. اين طرح روش آموزش صحبت كردن به بلبل ها بود! ايشان بلبلي را هم همراه برده بود و ادّعا مي كرد كه حرف مي زند ولي به خاطر ترس از جمعيّت از نطق كردن وامانده است.
مقاله هايي وجود دارند كه در آن ها رفتار نوابيغ مورد بررسي قرار گرفته اند. مثل مقاله ]يك[ كه در آن چنين آمده است : «يكي از مشخصه هاي نوابيغ رياضي، مانند ساير انواع نوابيغ، اين است كه به موفّقيت هاي كوچك قانع نيستند. حل مسائل معمولي آن ها را راضي نمي كند چرا كه دون شأن آن هاست. مي خواهند حرف مهم بزنند يا پنبه حرف هاي مهم را بزنند. بيشتر دوست دارند مسائلي را حل كنند كه ديگران ثابت كرده اند نمي توان آن ها را حل كرد ... خلاصه مي خواهند كاري بكنند كارستان. و از حيث شجاعت و بلند پروازي دست كمي از دانشمندان درست و حسابي ندارند. ولي متأسفانه شباهتشان با نوابغ واقعي، در همين يك صفت خلاصه مي شود.» براي علاقه مندان، مطالعه اين مقاله را پيشنهاد مي كنيم. نويسنده آن Underwood Dudley همان نويسنده كتاب هاي ]1[ و ]2[ است. ايشان بيش از ربع قرن است كه مشغول مطالعه رفتار و كردار نوابيغ رياضي هستند.
3. نوابيغ و پخش نظراتشان
* مراجعه به هر جا و هر كس
اغلب نوابيغ چيز زيادي از رياضي نمي دانند ولي علاقه مندند در اين زمينه كار كنند. شايد بپرسيد اصلاً چرا رفتيم سراغ اين آدم ها؟ جواب را بايد مراجعه بيش از حدّ اين افراد به انجمن رياضي و نشريات وابسته به آن و مديران گروه هاي رياضي دانست. مثلاً به عنوان رئيس انجمن رياضي لااقل از دفتر پنج مقام مختلف مملكتي براي بررسي ادّعاي فقط يكي از ايشان نامه هائي همراه با ضمايم فراوان رسيده است (به پيوست 3 مراجعه شود). راستش اين افراد خيلي تنها هستند. يكي از آنها (X) نوشته بود : «از اين كه با شما بزرگوار در ارتباط هستم از ته دل خوشحالم و اميدوارم اين ارتباط هم چنان پايدار باشد و از اين حالت يك طرفه شدن خارج شده و .... رياضيدان هاي بزرگ به حق نمي توانند وقت كافي براي رسيدگي به اين موضوعات بگذارند. دانشجويان رياضي نيز اغلب نمي دانند كه چنين افرادي هم وجود دارند. البته مشكل به اين جا ختم نمي شود. بين نوابيغ بعضاً كساني يافت مي شوند كه مستعد ايجاد مشكلات بسيار بزرگي براي رياضيدانان و بقيّه آدم ها هستند و اگر در برخورد با اين افراد دقّت لازم را به عمل نياورند بايد منتظر يك دردسر خيلي بزرگ باشيد كه در ادامه مقاله بيشتر متوجّه اهميّت موضوع خواهيم شد.
همان طور كه قبلاً اشاره شد يك گروه عمده از نوابيغ، تثليت گرها هستند كه اغلب آنها در دوران دبيرستان با مسأله تثليث مواجه مي شوند. مي دانيم كه ثابت شده است تيليث زاويه تنها با خط كش و پرگار امكان پذير نيست. مثلاً به كتاب «رياضيات چيست» (دو) فصل سوّم صفحات 147 و 148 رجوع كنيد. ولي اين افراد يا نمي دانند كه چنين اثباتي وجود دارد و يا نمي توانند معناي «امكان پذير بودن» در رياضيات را درك كنند. آيا تا به حال با كسي مواجه شده ايد كه متوجّه نشود فقط با يك شمع و يا با يك چراغ موشي نمي توان يك تيرآهن را گداخت؟!
در برخورد با يك تثليت گر، خواندن روش تثليت وي عملاً كار بيهوده اي است. علاوه بر اين، اين افراد معمولاً نمودارهاي پيچيده اي رسم مي كنند كه سر درآوردن از آن ها كار سختي است. جالب اينجاست كه حتّي وقتي اثبات امكان ناپذير بودن تثليت را برايشان بفرستيد باز هم اصرار دارند كه روش آن ها مورد مطالعه قرار بگيرد! نمونه اي از اين افراد خانم Z (دبير رياضي) بود كه پس از ارائه برهان توسّط يكي از نويسندگان (پيوست 2) باز هم اصرار بر خواندن مقاله اش داشت. ايشان حتّي تهديد كرد كه اگر مقاله اش را نخوانيم ما را به صاحب شب قدر مي سپارد.
* مراجعه به مقامات
يكي ديگر از ويژگي هاي نوابيغ اين است كه براي ثبت تئوري خود سراغ مقامات و مسئولين رده بالاي كشوري مي روند و حتّي ممكن است به بالاترين مقام كشور نيز رجوع كنند. يك نمونه از اين افراد آقاي U است كه ادّعا مي كند فرضيه گلدباخ را ثابت كرده است. ايشان براي اثبات ادّعاي خود حتّي به رهبر و رئيس جمهور و رئيس قوّه قضائيه نيز نامه نوشته اند. گوشه هايي از نامه پرسوز و گداز اين سودازده رياضي را برايتان مي آوريم :
« ... كار جديدم اثبات فرضيه تاريخي گلدباخ است. اين فرضيه به مدّت 261 سال لاينحل باقي مانده بود و دانشمندان نامداري چون اولر، گاوس، ويتوگرادف و هزاران رياضي دان ديگر در طول اين 5/2 قرن براي حل آن كوشيدند ولي ناكام ماندند .... بنده پس از دوازده سال تلاش در سال 1380 (سال مولي علي (ع)) موفق به اثبات قطعي آن گرديدم. اثبات بنده در 286 مركز علمي و دانشگاهي جهان بررسي و كوچكترين ايرادي بر آن وارد نگرديد. البتّه آمريكا پرداخت جايزه 1 ميليون دلاري بنده را مشروط به پذيرش تبعيت آمريكا نمود ....»
نوابيغ ممكن است هر كدام به تنهائي به مراجع زيادي رجوع كنند كه با اين عمل با توجّه به نامهه اي مختلف موجب اتلاف وقت بزرگي مي شوند. مثلاً موردي به نام آقاي X مقاله خود را به 100 مرجع مختلف فرستاده بود كه به قول خود چون از نوشتن همه آن ها عاجز بود به ناچار به دستگاه كپي متوسّل شده بود! اين آدم ها از رجوع به مقامات و مسئولين خسته نمي شوند و اگر در برخورد با اين آدم ها دقّت نكنيم ممكن است دچار يك دردسر اساسي شويم. مثلاً يكي از اساتيد دانشگاه در جواب يكي از همين نوابيغ مقاله اي را برايش فرستاده بود كه به خاطر اين كار آن شخص ايشان را به دادگاه كشاند.
* انتشار جزوات و كتاب ها
در برخي موارد نوابيغ براي عرضه نظريه هاي به قول خود «شگفت انگيزشان» دست به نشر كتاب در تيتراژ چند هزار جلدي مي زنند. حداقل دو مورد آن را اخيراً در كشورشاهد هستيم. يكي از اين دو نفري كه كتاب منتشر كرده است يك دانش آموز مقطع پيش دانشگاهي به نام Y است كه ادّعا مي كند :
«جلد اوّل اين كتاب علاوه بر بعد رياضياتش، بعد ديگري نيز دارد كه استفاده از آن در بحث هاي فلسفي و عرفاني از جمله اثبات روح، برزخ و حقيقت زنده شدن مردگان مي توان نام برد و ....»
و ديگري نيز كه كتاب خود را در دوران دبيرستان نوشته است، ادّعا مي كند كه :
«... در خلال اين تحقيقات موّفق به كشف رياضي اثبات وجود وحدانيّت خداوند متعال نيز شدم كه اميدوارم جوّ به خواب رفته علمي كشور را بيدار نمايد و ....» (X).
حتماً تا به حال خبر كشفيّات جديد در علم را از رسانه هاي گروهي از جمله اخبار سراسري شنيده ايد. ما مواردي را سراغ داريم كه اين افراد از طريق همين رسانه ها كه مردم، بسياري به بخش خبرهاي علمي آنها اعتماد دارند، خبر به اصطلاح كشفيات خود را به اطلاع عموم مي رسانند. مثل خبر حل فرضيه گلدباخ توسط آقاي X كه حداقل از يكي از شبكه هاي تلويزيوني پخش شده است. هم چنين ايشان چندين مصاحبه مطبوعاتي چاپ شده در روزنامه هاي كثيرالانتشار را در پرونده خود دارد.
خلاصه اين كه اگر پاي درددل بعضي از آن ها بنشينيد، ممكن است يك نطق مفصّل در مورد فرار مغزها به خاطر عدم حمايت از نابغه هائي مثل ايشان بكنند. اخيراً اغلب آن ها اين ادّعا را نيز بر ادّعاهاي فبلي خود اضافه كرده اند. مثل آقاي U كه حتّي ادّعا مي كرد از كشور آمريكا و انگلستان دعوتنامه براي ايشان و خانواده شان فرستاده شده و به ايشان ويزاي آمريكا همراه با چهار بليط مجّاني هواپيما پيشنهاد كرده اند. وي يك ديسكت حاوي اين ادّعا را به همه جا فرستاده بود كه ما با ديدن يك ديسكت متوجّه شديم موضوع چيزي نيست به جز چند پيام تبليغاتي كه براي شركت در قرعه كشي براي اخذ ويزا و يا مسافرت تفريحي معمولاً به تمامي كاربران Yahoo فرستاده مي شود!
راه هاي پيشنهادي براي مواجهه با نوابيغ
با توضيحاتي كه مطرح شد، حدس مي زنيم همه شما خوانندگان مثل ما معتقديد بهتر است فكري به حال اين افراد بكنيم تا هم بسياري را از درگير شدن با آن ها نجات دهيم و هم خود اين افراد دست از «آب در هاون كوبيدن» بردارند. مثلاً يكي از ايشان كه دبير رياضي هم است، ابراز مي دارد :
«اكنون بنده نه تنها از سال ها زحمت و تحقيقات ام خوشحال نيستم بلكه به شدّت غمگينم و فكر مي كنم راه اشتباهي رفته ام كه جذب علم و دانش و افتخار آفريني براي كشورم شده ام. چون از اوّلين روز اتمام اثبات و اعلام آن به دانشگاه ها تمام اضافه كاري ها و كمك درآمدها و كلاس هاي اضافه ام را تعطيل كرده و علاوه بر آن مخارج بسياري نيز در اين راه هزينه نمودم. البتّه هراسي نداشتم چون علاوه بر افتخار كشورم، يك ميليون دلار جايزه را نيز در دستم مي ديدم. لذا از قرض كردن نيز هراسي نكردم. امّا اكنون خوار و خفيف شده ام. هر روز از صاحب خانه فرار مي كنم كه اجازه چند ماه را نپرداخته ام. به اكثر آشنايان بدهكارم و شايد چند روز ديگر جهت بدهي به زندان هم بروم ... به زندان بروم يا به آمريكا بروم و تبعه آنجا شوم (البته بليط هواپيما و كارت اعتباري نيز برايم فرستاده اند كه در ديسك همراه نامه موجود است) يا در كشورم بمانم و اثبات قطعي فرضيه گلدباخ را با خودم به آن دنيا ببرم ....» (U).
ما مخاطبين اين افراد را به چهار دسته تقسيم مي كنيم :
* دسته اوّل، كساني كه وقت كافي براي پاسخ گويي به اين افراد را ندارند. به ايشان توصيه مي كنيم همين مقاله را در پاسخ آن ها ارسال كنند. چه بسا با مطالعه اين مقاله بسياري از مدّعيان پي به اشتباه خود برده و كار خاتمه يابد.
* دسته دوّم، بعضي از رسانه ها هستند كه با پخش خبرهاي غلط يا چاپ كتاب هاي خالي از هر گونه بار علمي موجب گمراهي اذهان عمومي مي شوند. با توجّه به رسالت مهم رسانه ها در اطلاع رساني چاپ اين گونه خبرها از طرف برخي از اين رسانه ها بسيار تأسف برانگيز است. رسانه ها قبل از نشر هر گونه خبر علمي بايد آن را توسط يك كارشناس مورد بررسي قرار دهند و در صورت اطمينان از صحّت، اقدام به پخش آن نمايند.
* دسته سوّم، دفاتر مقامات و مسئولين مملكتي است كه تصوّر مي كنيم در موارد بسياري تشخيص اين عدّه از نوابيغ برايشان كاري دشوار است. مثلاً يكي از مسئولان با ارسال ادّعاي آقاي X كه قبلاً ديديم ادّعاي «نامرئي كردن فيزيكي اشيا را» داشت به وزير علوم، تحقيقات و فن آوري، نوشته بودند «به پيوست تصويرنامه آقاي X از محققين، نظريه پردازان و طراحان رياضي كشور تقديم مي گردد. نامبرده از نوجواني تا كنون موفّق به كشفيات و ارائه طرح هايي در زمينه علوم رياضي گرديده اند ليكن براي ادامه فعّاليت هاي خود نيازمند مساعدت و حمايت مي باشند. نامه پيوست و ضميمه آن خود گوياي تمام توانايي ها و نبوغ نامبرده است. انتظار دارم درخواست ايشان مورد نظر قرار بگيرد كه قطعاً در پيشبرد اهداف علمي ايشان در نگاهي وسيع تر، كشور ايران بسيار سودبخش خواهد بود.»
هم چنين از طرف دفتر يكي از مقامات بلندپايه كشور پي نوشتي درباره ادّعاي آقاي X به انجمن رياضي ايران نوشته اند : «از ارسال كتاب تأليفي آقاي X محقق جوان و عزيزمان تشكر و قدرداني مي شود. براي ايشان از خداوند بزرگ آرزوي توفيق بيشتر را دارم.» لذا به دفتر مقامات پيشنهاد مي كنيم اگر بررسي اين ادعاها برايشان مهم است، از تعدادي از كارشناسان دعوت كنند كه به رسيدگي آن ها بپردازند. انجمن هاي علمي مي توانند معرّف اين كارشناس ها باشند.
* دسته چهارم، كساني كه علاقه مند به اين مسائل هستند و وقت كافي براي رسيدگي به آن ها را دارند. اگر شما هم جزء اين گروه هستيد، پيشنهاد مي كنيم مقاله (يك) را مطالعه كنيد. همان طور كه گفتيم نويسنده مقاله فوق حدود 25 سال در اين زمينه كار كرده و راه هاي مختلفي را در برخورد با اين افراد امتحان كرده است. ايشان نتيجه تجربيّات خود را در اين مقاله چنين بيان مي كند :
«سرانجام وقت آن رسيده كه بگويم با تثليت گرها چگونه بايد برخورد كرد. امّا بگذاريد اوّل بگوييم چگونه نبايد برخورد كرد. يك راه خلاصي موقّت از چنگ تثليت گرها آن است كه بگوييد : خوب تا اينجايش قبول، امّا مي دانيد كه بايد براي درست بودنش برهان داشته باشيد. يعني يك سري حكم ها و استدلال هايي نظير آنچه در كتاب هندسه قديميتان داشتيد. تثليث گر از نزدتان مي رود ولي به همراه برهان برمي گردد. در اين مرحله ممكن است بگوييد : خوب، حالا نگاهي به آن بياندازيم، اشتباه آن را بيابيد و به تثليت گر گوشزد كنيد.
تثليث گر اين بار هم مي رود ولي باز همراه با برهان تجديدنظر شده اي برمي گردد كه طولاني تر، پچيده تر و يافتن اشتباهش دشوارتر است. تجديدنظرهاي پياپي در برهان، كار را به جايي مي كشاند كه ديگر نتوانيد يا نخواهيد اشتباه آن را پيدا كنيد. قدم بعدي كه آن نيز خطاست، اين است كه بگوييد :
راستش من وقت بررسي اين برهان را ندارم ولي مي دانيد كه شخصي به نام وانيتيسل در سال 1837 ثابت كرده كه زاويه را نمي توان با خط كش و پرگار تثليث كرد. برهان او موجود است، اين هم برهان شما؛ هر دوي اين ها نمي توانند درست باشند؛ پس چاره اي نيست جز اين كه شما در برهان وانيتيسل اشتباهي پيدا كنيد. اين كار هم تثليثت گر را از سرتان باز مي كند. ولي او دير يا زود بر مي گردد با رديه اي بر برهان وانتسل در قالب چنان عباراتي كه درك معني شان ناممكن است. هيچ چيز نمي تواند راه را بر تثليث گر از خود گذشته ببندد.
پس در برخورد با تثليث گر چه بايد كرد؟ به اوّلين نامه تثليث گر، اگر مطمئن شديد كه خوبي تقريب يا سادگي روش يا هوشمندي او در يافتن تقريبي جديد قابل توجه است، مودّبانه جواب بدهيد. به همراه نامه، برايش فهرستي كامپيوتري از اشتباهات موجود در ترسيم براي زاويه هاي مختلف بفرستيد. من معمولاً فهرست را براي 0 تا 180 درجه، با فواصل 3 درجه اي تهيّه مي كنيم. اين كار مهم است زيرا هنوز كامپيوتر قدرت آن را دارد كه احساس احترام و ابهتي در افراد ايجاد كند. همچنين با آن نامه چند تثليث تقريبي ديگر را بفرستيد با تذكّري از اين قبيل كه فكر كردم شايد علاقه مند باشيد ديگران چه تثليث هاي تقريبي به دست آورده اند. در سال هاي اخير با استفاده از اين روش ميزان موفّقيتم بالا رفته است. يادم هست كه اوّلين موفّقيّت تا چه حد مايه رضايت خاطرم شد. مهندسي در شهر نيوجرسي كتاب بزرگي با جلد مقوّايي در حجم بيش از 250 صفحه تهيّه كرده بود كه عنوان ماجراهاي هندسه روي جلد آن با حروف زركوب نقش بسته بود. به نظرم رسيد كسي كه اين همه براي تثليث مايه گذاشته باشد، راه نجاتي ندارد. ولي او ضمن پاسخ نامه ام نوشت : همين قدر كه توانسته ام به تقريبي برسم راضي هستم و ديگر آن را كنار مي گذارم. اين بار روحم از نفرين به دور ماند! اخيراً چند موفّقيّت ديگر هم داشته ام و شايد برخي از اين تثليت گرهاي لب فرو بسته، متقاعد هم شده باشند، اگر با اين روش كاري از پيش نرفت، آن وقت بي رحم باشيد. نامه و برخورنده اي بنويسيد، به اين قصد كه طرف از شما بدش بيايد. ديگر به هيچ قيمتي مزاحم شما نخواهد شد و شايد بخشي از نفرتش منجر به بي علاقگي نسبت به رياضيدانان و بي ميلي به ادامه كار تثليث شود، زيرا معمولاً انسان اگر بتواند، از كاري كه مايه آزارش شود خودداري مي كند. اگر همه همين روش را در پيش مي گرفتند نسل تثليث گرها تحليل مي رفت و منقرض مي شد. در آن صورت كساني كه سودازدگي جزء سرشتشان است مزاحم اقتصاد دان ها، فيزيك دان ها يا علماي الهيّات مي شدند و ما مي توانستيم در آرامش و امنيّت زندگي كنيم و مطمئن باشيم كه از اين پس هيچ سودازده اي به سراغمان نخواهد آمد. در اين جا به طور خاص در مورد تثليث گرها صحبت شده است، امّا حتماً شما آنقدر وارد هستيد كه با استفاده از آن، روش برخورد با ساير نوابيغ را نيز بيابيد.»
موخره، از خوانندگان محترم تقاضا مي شود اگر خاطره اي از نوابيغ دارند حدود يك يا دو صفحه به اينجانبان ارسال دارند تا در ضميمه اين مقاله بيايد. به پيوست نمونه اي از نامه هاي ارسال شده در رابطه با نوابيغ ضميمه شده است.
پيوست : چند نمونه از نامه هاي ارسالي درباره مدّعيان
* پيوست 1 : آقاي ... مقاله شما را در ادعاي كشف فرمول محاسبه محيط بيضي مشاهده كردم. به اطلاع مي رساند كه انجمن رياضي ايران بر اساس تجربه هاي قبلي به اين گونه مدعيان پيشنهاد مي كند كه با اساتيد دانشگاه ها مستقيماً مكاتبه نمايند. اما اين جانب خود به عنوان يك عضو هيأت علمي دانشگاه، نظرم را ذيلاً مكتوب مي نمايم.
لازمه محاسبه فرمول دقيق محيط بيضي محاسبه انتگرال هايي مانند انتگرال زير است كه ثابت شده است محاسبه آن بر حسب توابع معمولي امكان پذير نيست.
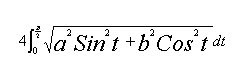اين فرمول با استفاده از فرمول پارامتري بيضي كه به صورت
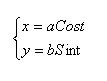است به دست مي آيد. و اين موضوع تقريباً در هر كتاب رياضيات عمومي (CALCULUS) نيز آمده است.متأسفانه بعضي از افراد معني امكان ناپذير بودن را متوجه نمي شوند و اغلب تلاش بيهوده در يافتن چنان فرمولهائي مي نمايند. اميدوارم كه جنابعالي معني آن را دريافته باشيد. باعث تأسف است كه بعضي از رسانه ها نيز بدون مشورت با متخصصين اقدام به چاپ يا نشر بعضي از «كشفيّات» مي كنند كه باعث توهم بعضي از افراد مي شود.
با احترام، سيد عباداله محموديان، رئيس دانشكده علوم رياضي، دانشگاه صنعتي شريف و رئيس انجمن رياضي ايران.
* پيوست 2 : خانم ... با سلام، مقاله شما را مشاهده كرديم و به اطلاع شما مي رسانيم كه ثابت شده است تثليت زاويه به كمك خط كش و پرگار امري است امكان ناپذير. بدين منظور شما را مثلاً به صفحات 147 و 148 از «كتاب رياضيات چيست؟» تأليف ريچارد كورانت كه ضميمه نامه است ارجاع مي دهيم. براي اطّلاع بيشتر پيشنهاد مي كنيم فصل سوم كتاب فوق را مطالعه بفرمائيد.
با اميد سلامتي روزافزون شما، سيد عباداله محموديان، استاد دانشكده علوم رياضي دانشگاه صنعتي شريف.
* پيوست 3 : استاد محترم جناب آقاي دكتر ... معاون محترم پژوهشي وزارت ...
با سلام، احتراماً عطف به نامه مورخه ... شماره ... به استحضار مي رسانم كه كتاب ارسالي (تأليف آقاي ...) توسط دو نفر داور مورد بررسي قرار گرفت. نظر ايشان در ضميمه آمده است. متأسفانه ظرف چند ماه اخير كه اينجانب رياست انجمن رياضي ايران را به عهده گرفته ام چند مورد مشابه اين نامه به بنده ارسال شده است (بعضي از آن ها مانند كتاب فوق الذكر از چندين اداره مختلف). رسيدگي به آنها بسيار وقت گير است. در صورتي كه خود مكتوبات نشان از بي اساس بودن «نظريه» دارد. مثلاً همين نويسنده ادعا دارد كه تا پايان سال (1382) «تئوري نامرئي كردن فيزيكي اشياء را كامل» مي كند. جالبتر اين كه بعضي از مقامات نيز اين ادعا را «گوياي تمام توانائي ها و نبوغ نامبرده» مي دانند.
پيشنهاد اينجانب اين است كه اگر اين گونه ادعاها براي دفتر جنابعالي مهم است، موسسه اي تأسيس بفرمائيد تا آن ها را بررسي كند. در آن صورت اگر لازم تشخيص بدهيد انجمن مي تواند متخصصين امر را براي آن موسسه پيشنهاد كند.
با تقديم احترام، سيد عباداله محموديان، رئيس انجمن رياضي ايران و رئيس دانشكده علوم رياضي، دانشگاه صنعتي شريف
رونوشت : به چهار مرجع ديگر كه كتاب فوق را فرستاده بودند.
مراجع
]يك[ اندروود دادلي، با تثليث گرها چگونه برخورد كنيم، (ترجمع محمد باقري) نشر رياضي : مجله رياضي مركز نشر دانشگاهي، سال 2 شماره 3 آذر 1368 صفحه 227- 222.
]دو[ ريچارد كورانت و هربرت رابينز، رياضيات چيست؟ ترجمه سيامك كاظمي. تهران : نشر ني، 1379.
[1] Underwood Dudley, A Budget of Trisections, Springer-Verlag, New York, 1987.
[2] Underwood Dudley, Mathematical Cranks, Mathematical Association of America, Washington, D.C. 1992.
۲ نظر:
سلام
خیلی زیباست و وضع جامعه نجومی رو خوب پوشش میده.
حالا تونستم وضع طرفو بفهمم.
هادی
.....
حالا فهمیدم چه طوری باهاش برخورد کنم........
ارسال یک نظر